Узнайте, как понять и найти среднюю линию треугольника. Разберитесь в свойствах и способах нахождения средней линии треугольника. Используйте эти знания для решения геометрических задач.
Как понять средняя линия треугольника?
Треугольник - это геометрическая фигура, состоящая из трех отрезков, соединенных тремя точками, которые не лежат на одной прямой. В треугольнике можно выделить различные виды, такие как равнобедренный, равносторонний и прямоугольный треугольники.
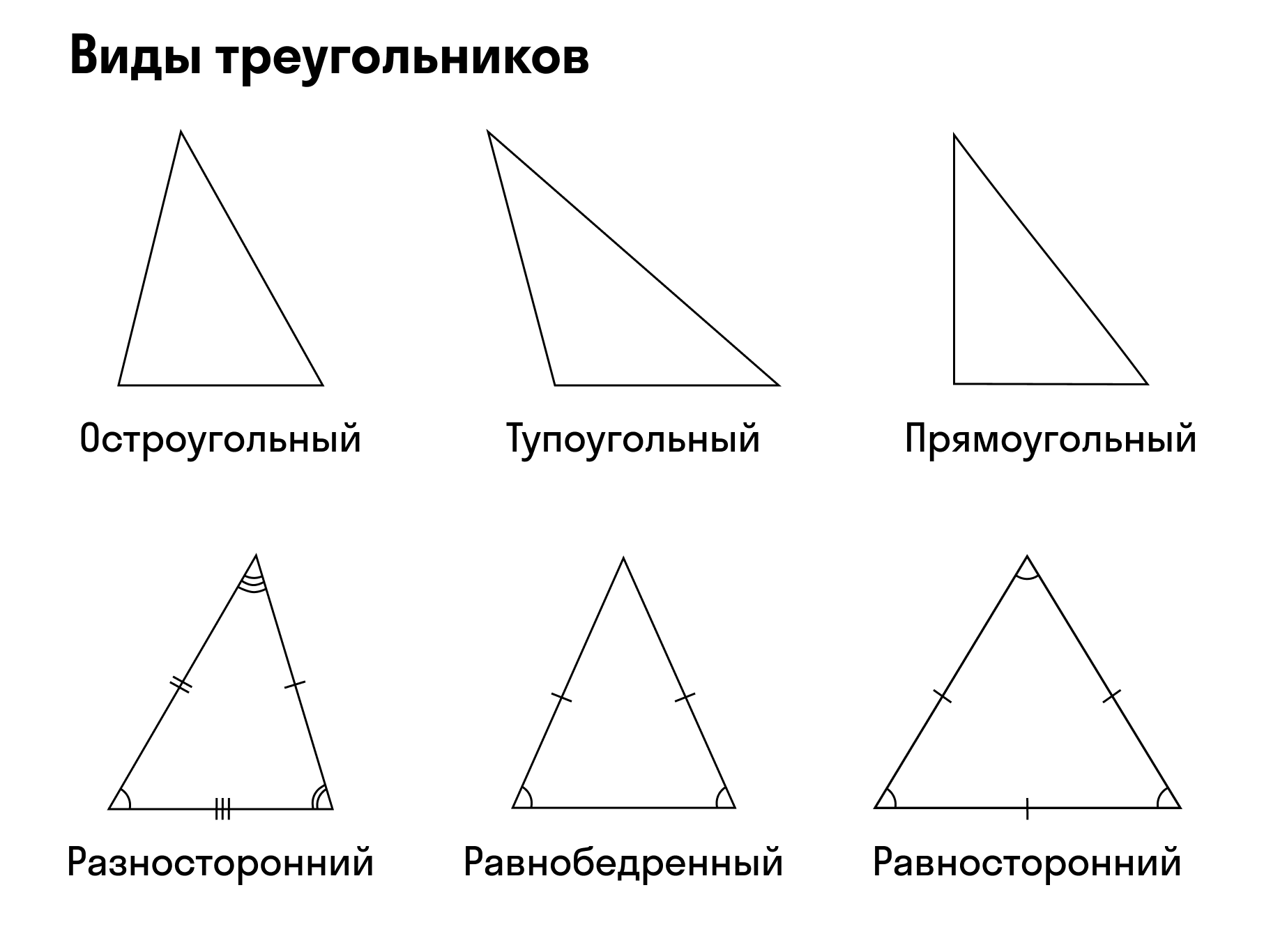
Виды треугольников
Равнобедренный треугольник имеет две равные стороны, которые называются боковыми сторонами, и третью сторону - основание.
Равносторонний треугольник имеет все стороны равными друг другу.
Прямоугольный треугольник имеет прямой угол, то есть угол в 90°. Одна из сторон прямоугольного треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны - катетами.
Правильный треугольник, который является и равносторонним, и равноугольным, имеет все стороны и углы равными и составляющими 60°. В равностороннем треугольнике средняя линия является и биссектрисой, и медианой.
Свойства треугольников
Треугольники обладают рядом свойств, которые помогают нам анализировать и решать задачи с ними. Например, в равнобедренном треугольнике углы, прилегающие к равным сторонам, также равны. В прямоугольных треугольниках можно использовать геометрические тождества для нахождения сторон и углов.

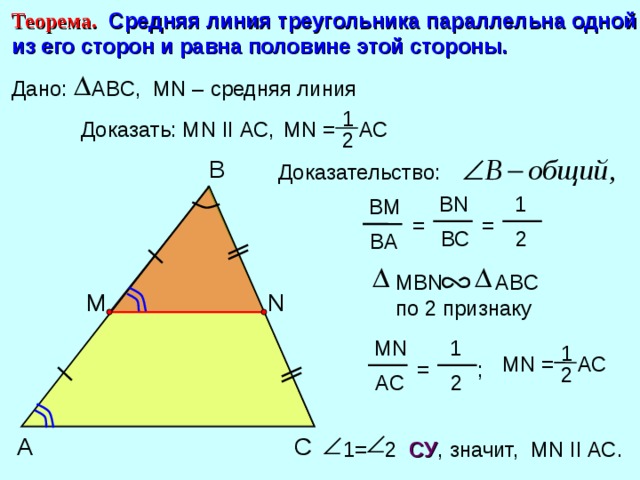
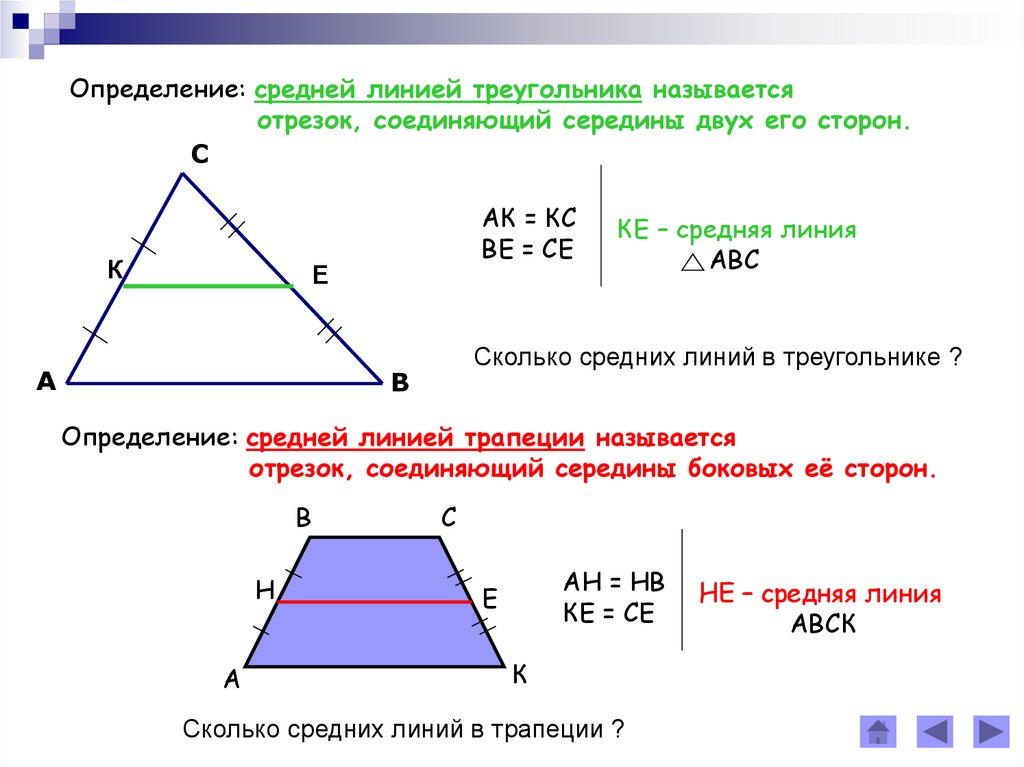
Понятие средней линии треугольника
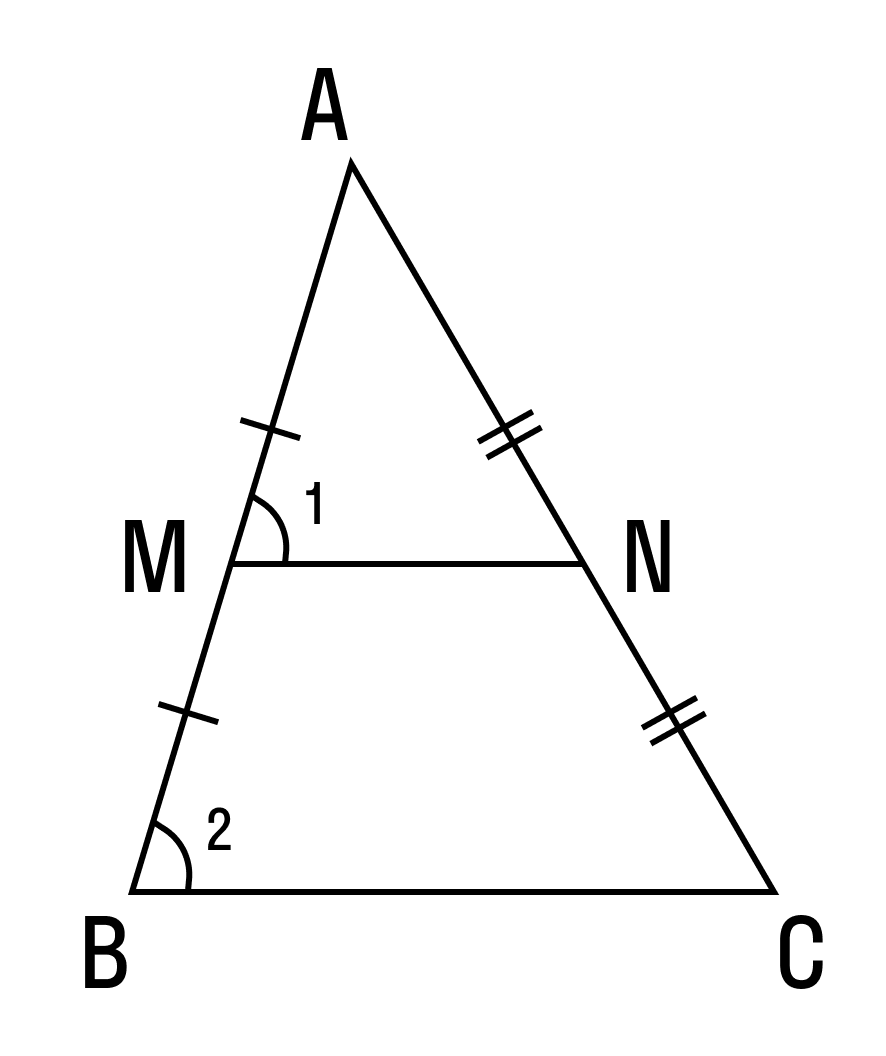
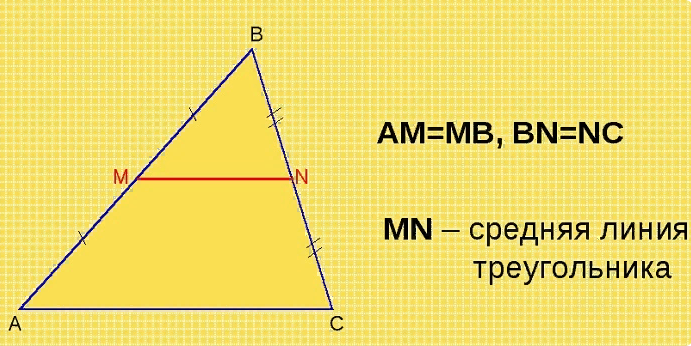
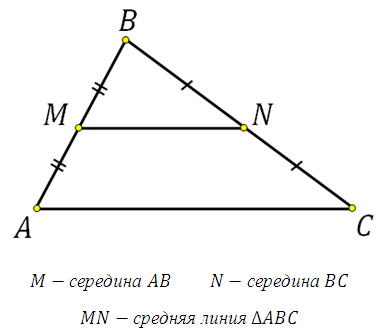
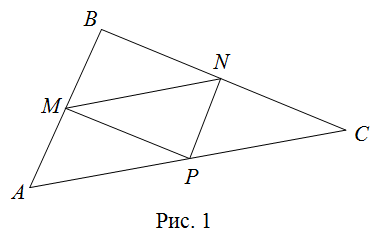
Средняя линия треугольника - это отрезок, который соединяет середины двух сторон этой фигуры. В любом треугольнике можно провести три средние линии. Основанием этой линии считается сторона, параллельная ей.
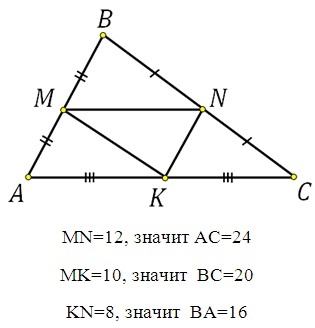
Как найти среднюю линию треугольника?
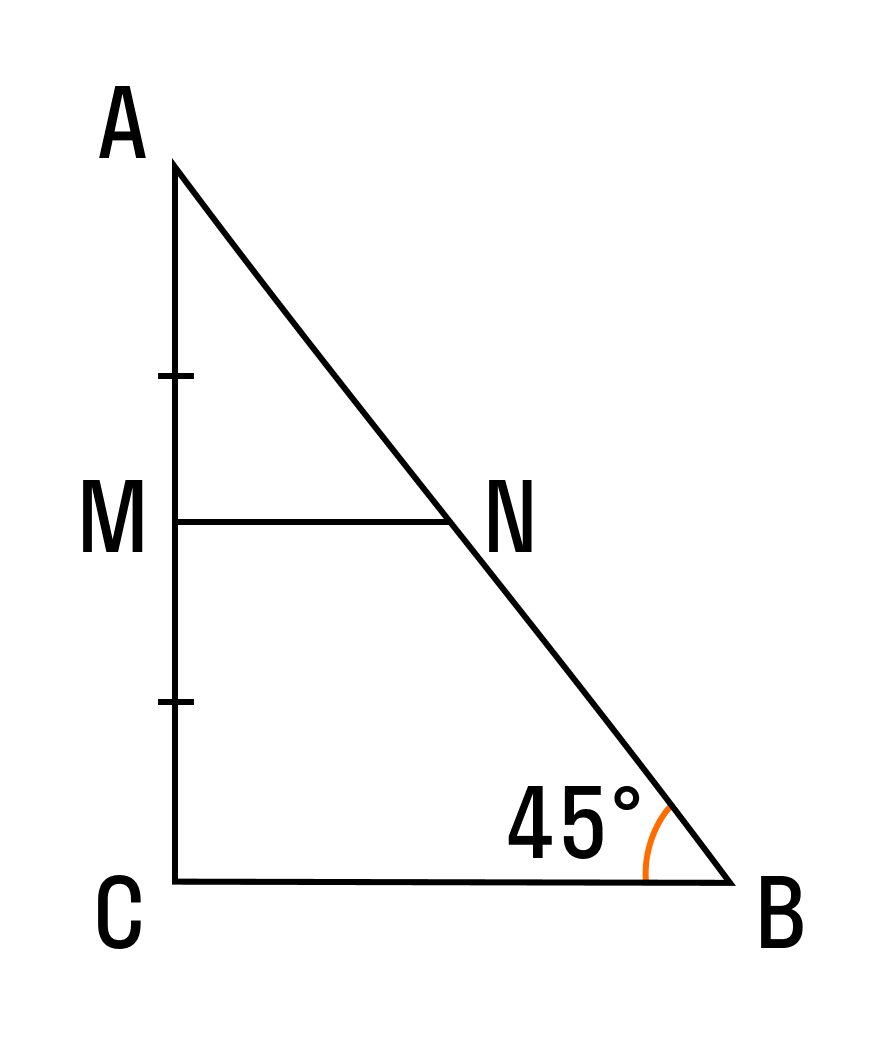
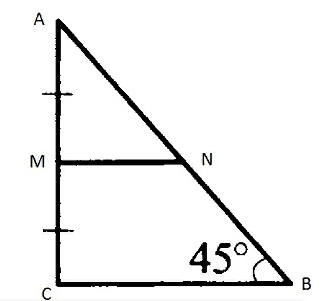
Для нахождения средней линии треугольника необходимо взять основание и разделить его пополам. Так, в прямоугольном треугольнике, средняя линия будет равна половине основания.
Свойства средней линии треугольника
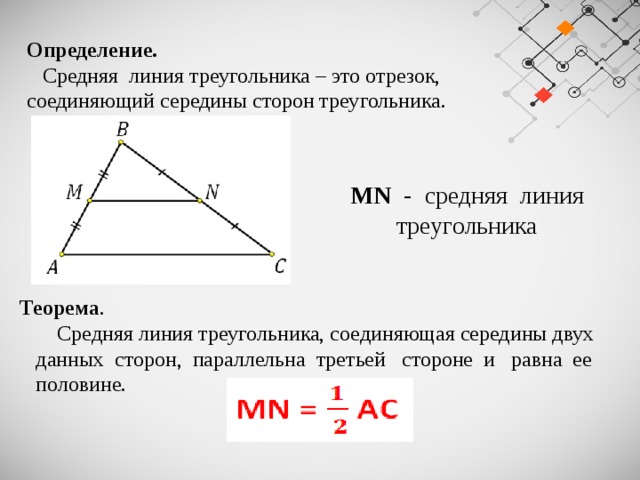
Средняя линия треугольника имеет следующие свойства:
- Она параллельна основанию треугольника.
- Она делит стороны треугольника пополам.
- Средняя линия отсекает треугольник, подобный исходному, с коэффициентом 1/2.
Средняя линия треугольника является важным понятием в геометрии и широко используется при решении задач, связанных с треугольниками и другими фигурами. Понимание ее свойств и способов нахождения позволяет более эффективно решать геометрические задачи.