Понятие средней линии треугольника

Узнайте, что такое средняя линия треугольника и как ее найти. В статье рассмотрены виды треугольников, определение средней линии и ее свойства, а также приведен пример задачи по нахождению длины средней линии треугольника.

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

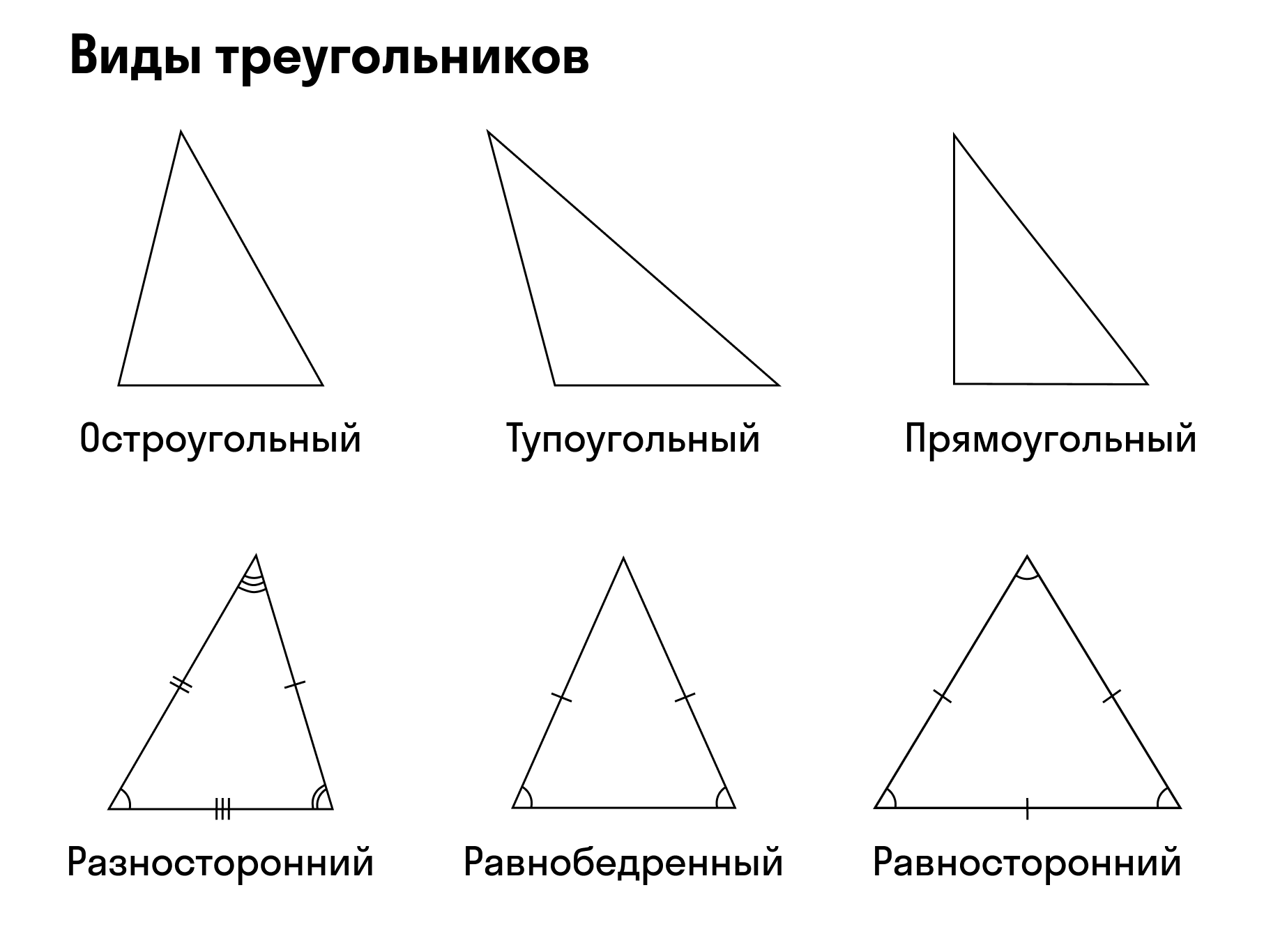
Виды треугольников

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

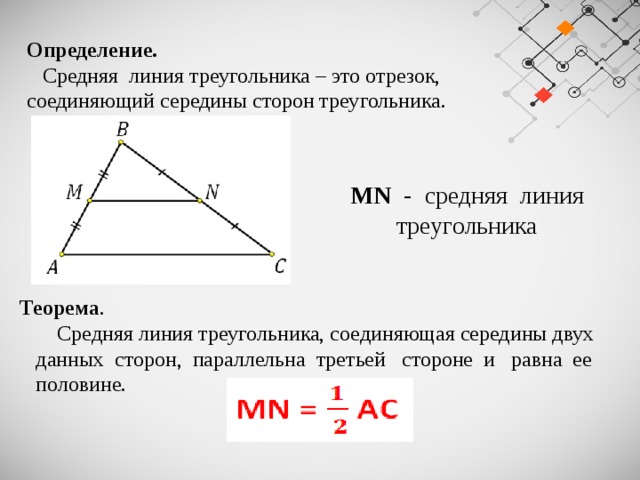
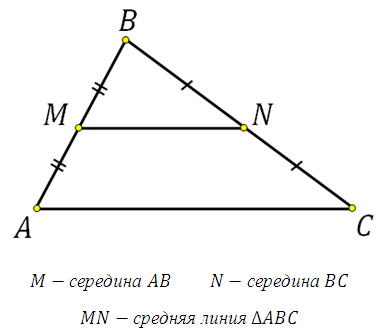
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

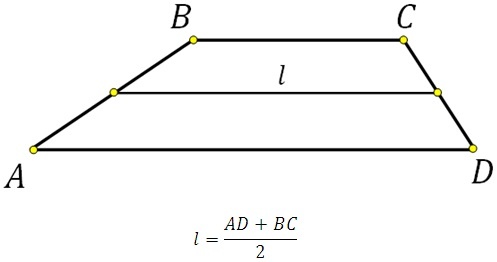
Основанием считается сторона, которой параллельна средняя линия.

Понятие средней линии прямоугольного треугольника

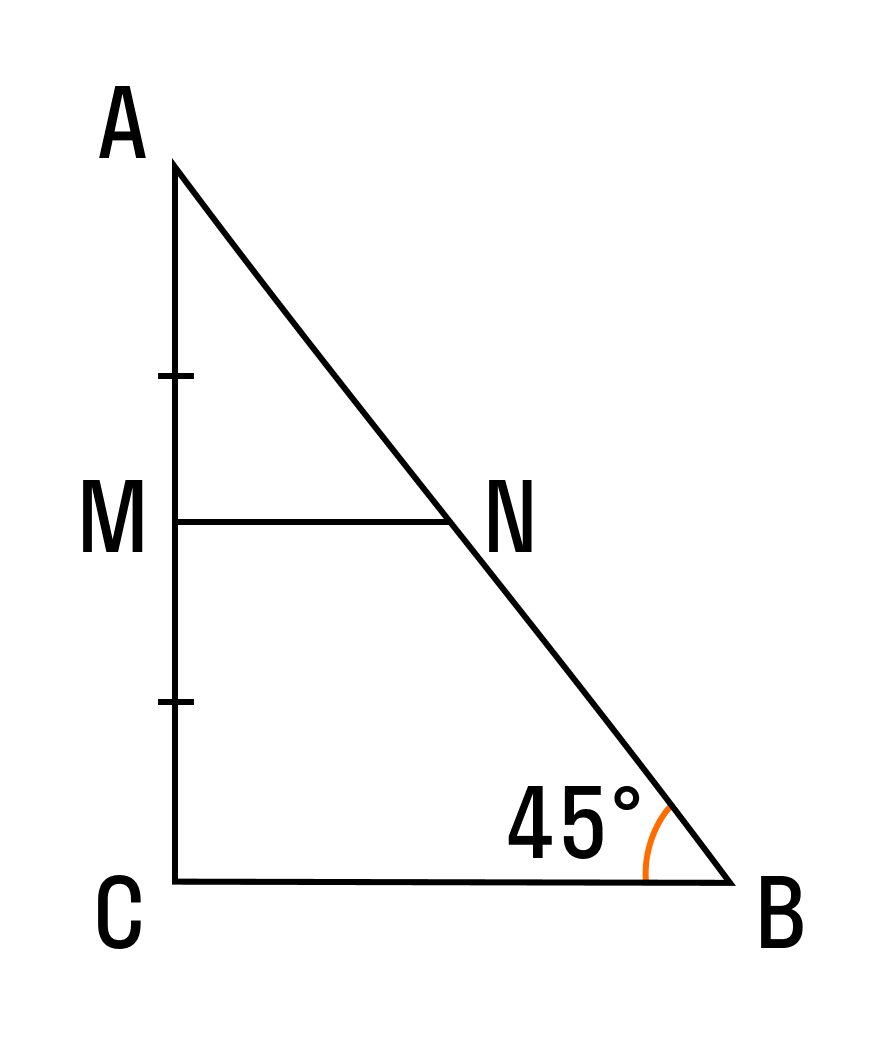
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

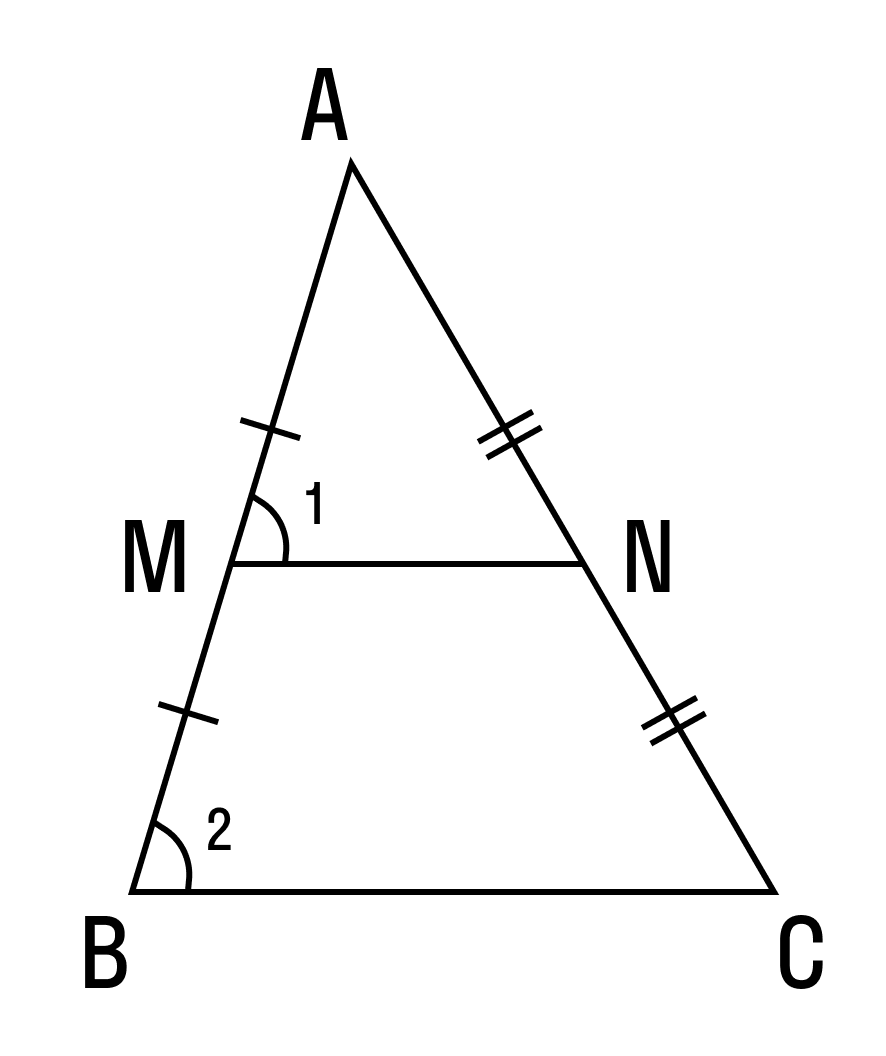
Свойства средней линии треугольника

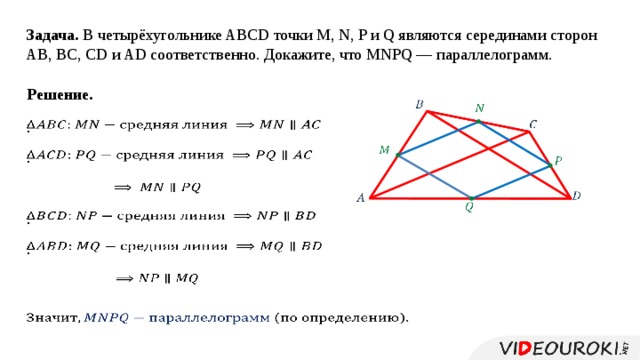
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

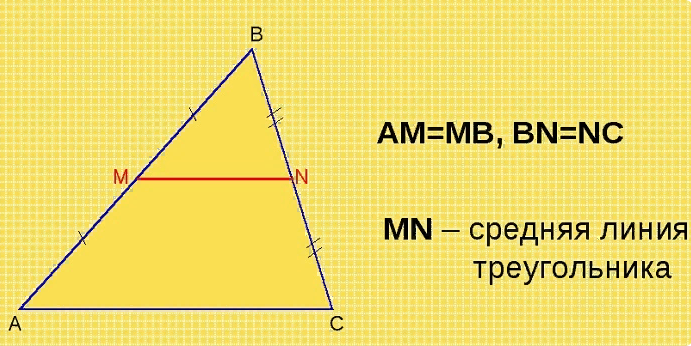
Теорема о средней линии треугольника

Теорема о средней линии треугольника утверждает, что средняя линия треугольника параллельна третьей стороне и её длина равна половине длины этой стороны.

Таким образом, средняя линия треугольника является половиной медианы и предмедианы треугольника.

Пример задачи

Рассмотрим типичную задачу по нахождению средней линии треугольника.

Задача: Найти длину средней линии треугольника, если известны длины его сторон.

Решение: Для нахождения длины средней линии треугольника, необходимо знать длины двух его сторон.

Пусть a и b — стороны треугольника, а c — сторона, к которой параллельна средняя линия.

Тогда, согласно теореме о средней линии, длина средней линии равна половине длины стороны c.

Таким образом, длина средней линии треугольника равна c/2.

Заключение

Средняя линия треугольника является важным понятием в геометрии. Она помогает нам находить половину медианы и предмедианы треугольника, а также связывает середины двух его сторон. Зная длины сторон треугольника, мы можем легко вычислить длину средней линии и использовать эту информацию для решения геометрических задач.

Что нам скажет Википедия?

Медиана треугольника (лат. mediāna — средняя) ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.

Если A, B, C ― треугольник, и a = BC, b = AC, c = AB ― длины сторон (или просто стороны), то медианы, проведённые соответственно из вершин A, B, C к сторонам a, b, c, обычно обозначаются m_a, m_b и m_c.

Связанные определения:

• Точка пересечения медиан делит каждую медиану на два отрезка. Отрезок от вершины до точки пересечения называется предмедианой, а отрезок от точки пересечения до противоположной стороны постмедианой. В частности, можно сказать, что в любом треугольнике отношение предмедианы к постмедиане равно двум.

Основное свойство:

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Свойства медиан равнобедренного треугольника:

В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине. У равностороннего треугольника все три медианы равны.

Если медианы равнобедренного треугольника, проведённые к боковым сторонам, пересекаются под прямым углом, то косинусы углов при основании этого треугольника равны 1/√10, а косинус противоположного основанию угла равен 4/5.

Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония. В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон. Обратно, можно выразить длину произвольной стороны треугольника через медианы. Площадь S любого треугольника, выраженная через длины его медиан.