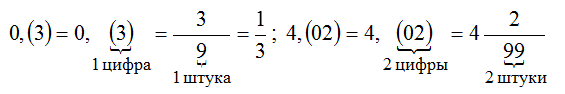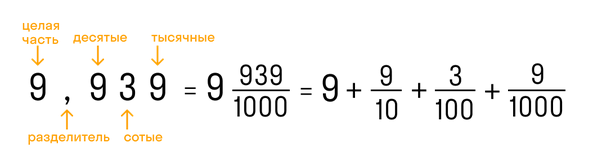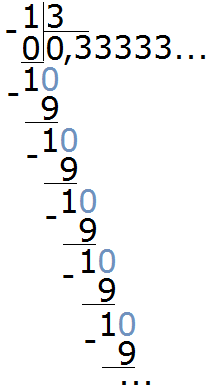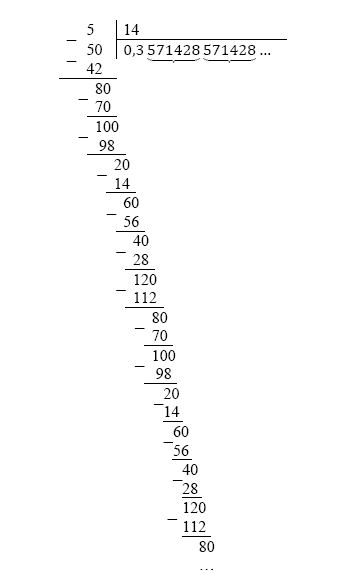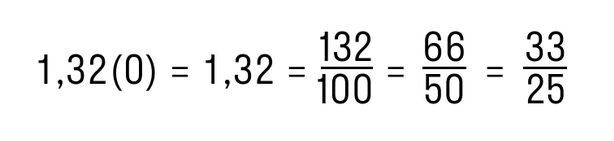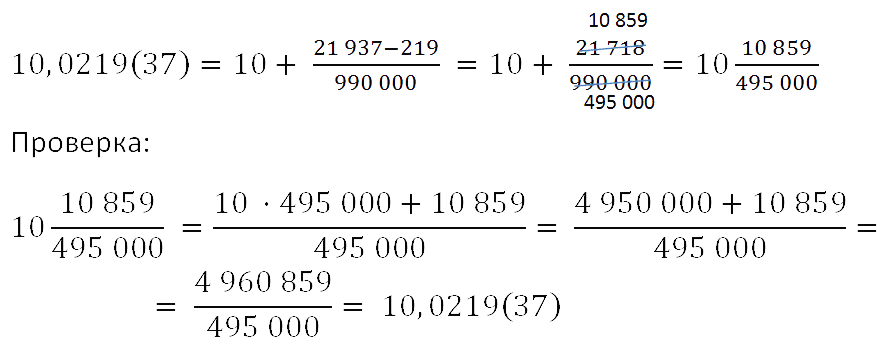Узнайте, что такое периодические дроби и как их записывать. Периодические дроби являются особой формой записи десятичных дробей, в которой некоторые цифры бесконечно повторяются. Мы рассмотрели примеры периодических дробей и их сокращенную запись. Виды периодических дробей, такие как чистые и смешанные, были также рассмотрены. Периодические дроби играют важную роль в арифметике и представлении рациональных чисел в десятичной форме.
Cодержание
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Эти дроби называются периодическими. В данной статье мы разберемся, что это за дроби и как с ними работать.

Получаем периодическую дробь
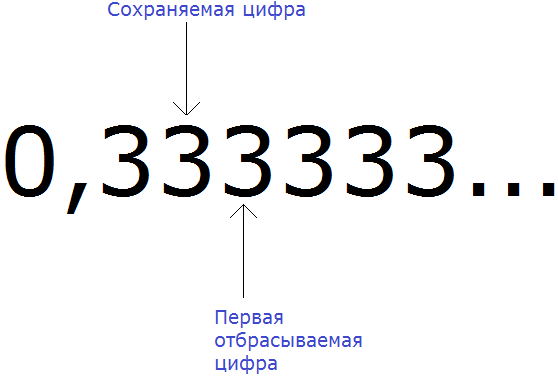
Рассмотрим пример деления числа 1 на 3. При делении мы получаем остаток 1, затем приписываем к нему 0 и делим 10 на 3. Этот процесс повторяется вновь и вновь, и в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому мы остановимся и сосредоточимся на периодической части.
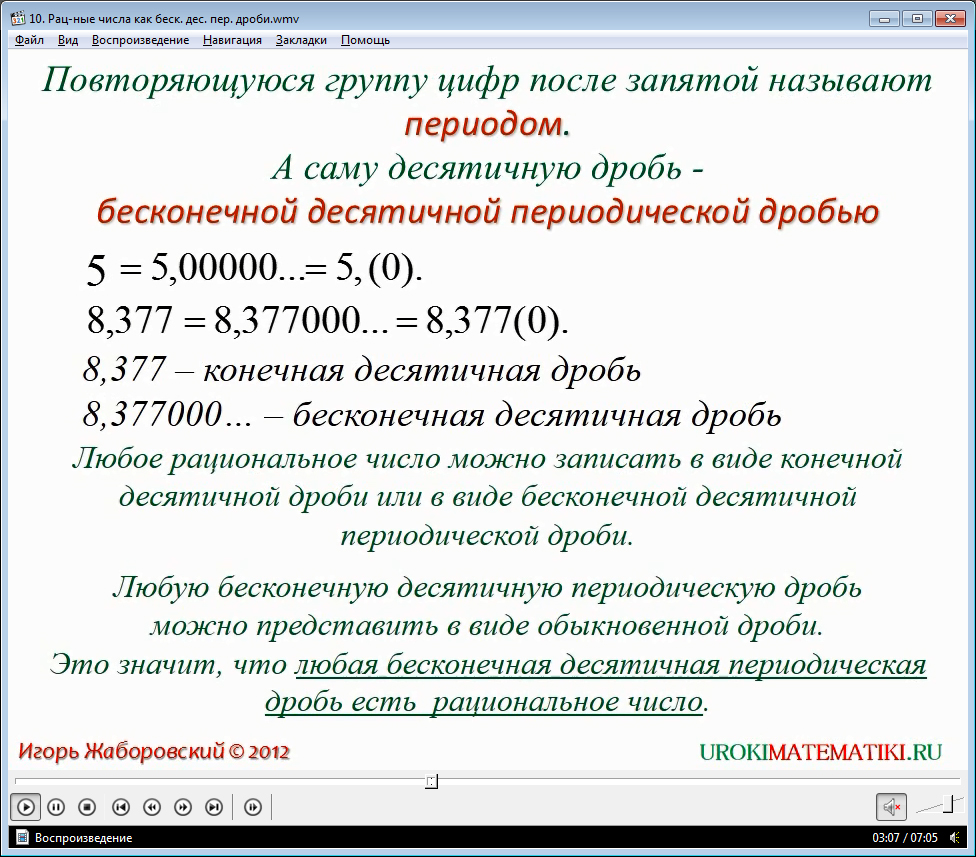
Периодические дроби состоят из периода цифр, который бесконечно повторяется. Период может состоять из одной цифры, например, в случае с дробью 0,33333..., период составляет цифра 3. Обычно такие дроби записывают сокращенно, где после целой части ставится запятая, а в скобках указывается период цифр.
Например, дробь 0,33333... сокращенно записывается как 0,(3), где период состоит только из цифры 3. Аналогично, дробь 0,6818181818... сокращенно записывается как 0,68(18), где период состоит из цифр 18.
Примеры периодических дробей
Давайте рассмотрим несколько примеров периодических дробей и их сокращенную запись.
Пример 1: 5/11
Разделим 5 на 11. В этом случае период состоит из цифр 4 и 5, которые повторяются бесконечно. Сокращенная запись будет выглядеть как 0,4(5), что читается как "ноль целых и сорок пять в периоде".
Пример 2: 15/13
Деление 15 на 13 дает период, состоящий из цифр 153846. Сокращенная запись для данной периодической дроби будет выглядеть как 1,(153846), что можно прочитать как "одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде".
Пример 3: 471/900
В этом примере период начинается после цифр 5 и 2. Сокращенная запись для данной периодической дроби будет выглядеть как 0,52(3), что читается как "ноль целых пятьдесят две сотых и три в периоде".
См. также
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смешанные.
Чистые периодические дроби начинаются сразу после запятой, например, 0,(9) или 0,999... При этом период состоит только из одной цифры. Чистые периодические дроби представляют числа, которые можно записать в виде обыкновенной (простой) дроби.
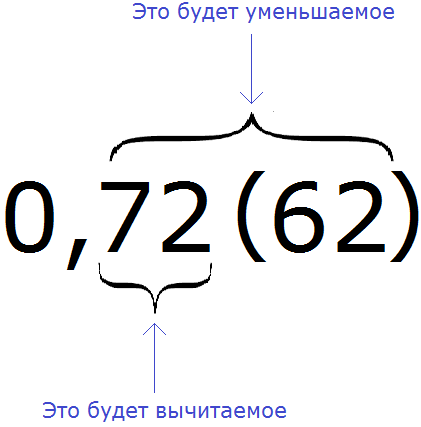
Смешанные периодические дроби имеют цифры, предшествующие периоду. Например, 1,3(18). При записи смешанной периодической дроби, числителем служит разность между числом, изображаемым цифрами, предшествующими второму периоду, и числом, изображаемым цифрами, предшествующими первому периоду.
Роль периодических дробей в арифметике связана с представлением рациональных чисел в виде десятичных дробей. Все рациональные числа можно представить либо в виде конечной десятичной дроби, либо в виде периодической дроби.
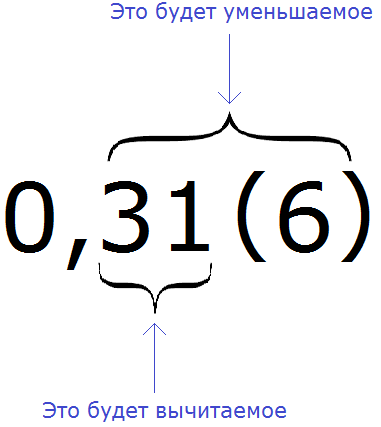
Заключение
Периодические дроби являются особой формой записи десятичных дробей, в которой некоторые цифры бесконечно повторяются. Мы рассмотрели примеры периодических дробей и их сокращенную запись. Виды периодических дробей, такие как чистые и смешанные, были также рассмотрены. Периодические дроби играют важную роль в арифметике и представлении рациональных чисел в десятичной форме.
Что нам скажет Википедия?
0,(9) или 0,999... ("ноль и девять в периоде") — периодическая десятичная дробь, представляющая число 1.
При использовании математических обозначений стоит понимать, что обозначения — это не есть сам предмет обсуждения, а всего лишь его обозначение. Два обозначения вполне могут обозначать один и тот же предмет. К примеру, запись 1/10 и 0,1 обозначают одно и то же число. Хоть это и разные записи, задают они один и тот же объект. Другой пример — 1/2 и 2/4. На этом примере видно, что разные обыкновенные дроби вполне могут задавать одно и то же число, и, таким образом, запись в виде обыкновенной дроби неоднозначна.
Тот факт, что запись в виде конечной десятичной дроби однозначна, является особенностью именно конечных дробей. Разные конечные дроби обозначают разные числа. Но работает это свойство только для конечного случая. В общем случае (где допускаются и конечные, и бесконечные десятичные дроби) две различные десятичные дроби могут представлять одно и то же число. Это связано с тем, что бесконечные дроби являются весьма непростым объектом, и многие свойства конечных на них не работают или работают не так. Примером такого неоднозначного представления являются 1 и 0, (9). Несмотря на то, что запись у них разная, они представляют собой одно и то же число, аналогично тому, как 1/2 и 2/4 представляют одно число.