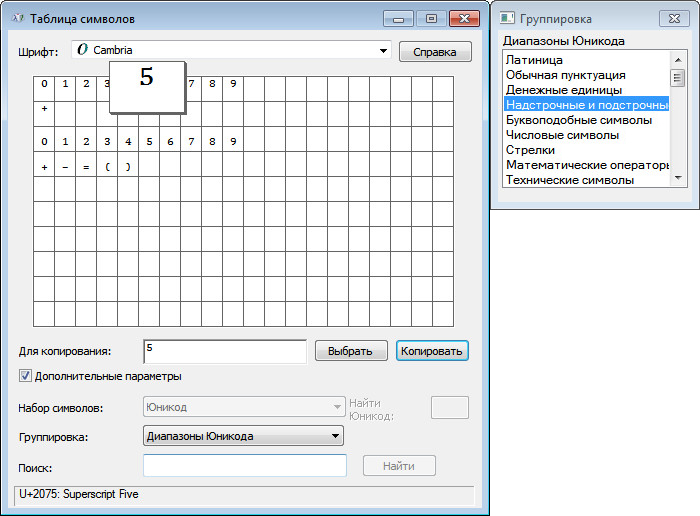
Числа бывают не только простые. Как записать степень числа символами на бумаге? Узнайте способы записи степени числа на клавиатуре с помощью комбинаций клавиш. Напишите степень числа в квадрате и в кубе с использованием кодов на клавиатуре.
Cодержание
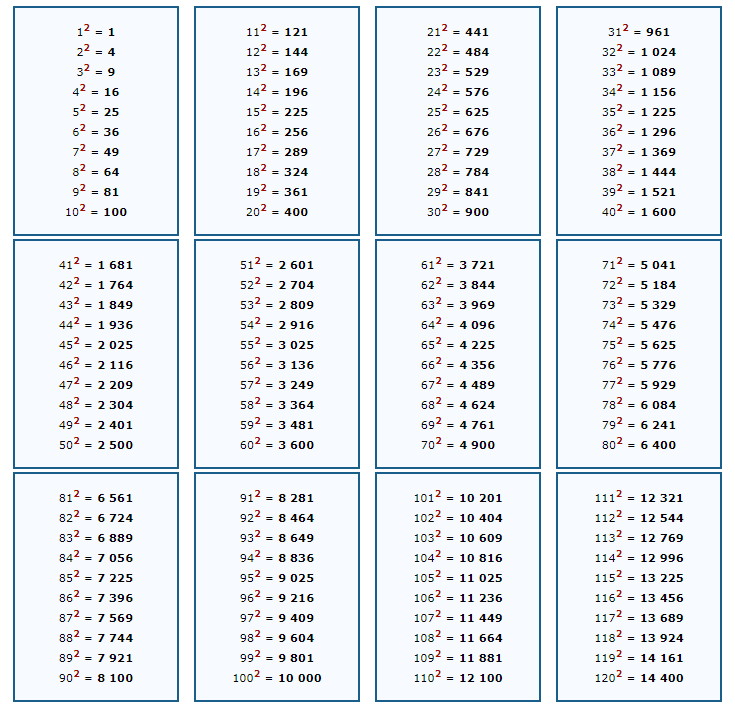
Числа бывают не только простые. Порой числа возводят в степень: в квадрат (во вторую степень), в куб (в третью), и вообще в любую другую степень. Как это записать на бумаге – понятно. Ставишь возле числа сверху еще одно дополнительное число «2», либо «3» или любое другое – вот вам и степень числа.

Два кода для написания степени в квадрате или в кубе
Проблема в том, что клавиатура не оснащена такой клавишей, которая позволила бы вот так просто поставить степень. Но для этого существуют специальные комбинации клавиш:
- «Alt+0178» – с ее помощью можно написать вторую степень (²);
- «Alt+0179» – используя эту комбинацию, можно написать третью степень (³).
Однако не все так просто, есть нюансы.
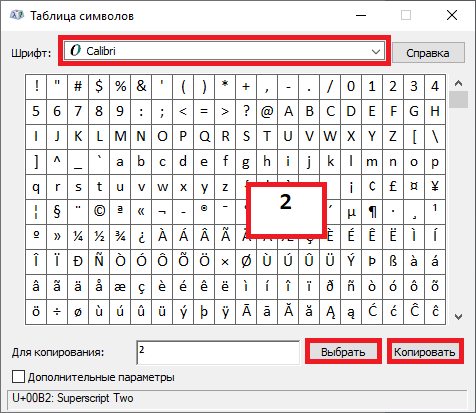
Как написать степень на клавиатуре с помощью кодов
- Перед тем как воспользоваться вышеперечисленными комбинациями, следует убедиться, что выставлен английский язык.
- Затем нужно активировать цифровую панель путем нажатия на «Num Lock». Такую панель называют еще малой цифровой клавиатурой.
- Поставить курсор в то место текста, куда требуется вставить степень.
- Удерживая клавишу «Alt», поочередно набрать цифры на малой клавиатуре, например, 0, 1, 7, 8. Отпустив «Alt», на экране сразу увидим степень 2 («в квадрате»).
- Также удерживая «Alt», можно последовательно нажать на малой цифровой клавиатуре цифры 0, 1, 7, 9. Отпустив «Alt», получим 3 степень («в кубе»).
См. также
Надстрочный знак в Word позволяет напечатать любую степень числа
Если вы работаете в текстовом редакторе Word и вам нужно написать степень числа, то проще всего воспользоваться специальной кнопкой, которая называется «Надстрочный знак». В современных версиях Word (например, в Word 2007, 2010, 2013 и 2016) такая кнопка находится на вкладке «Главная». Выделите знак, который должен стать степенью числа и нажмите на эту кнопку.
В результате вы получите число и степень. Нужно отметить, что в качестве степени можно использовать не только числа, но и буквы.
Если вы пользуетесь старыми версиями текстового редактора Word, например, Word 2003, то для того чтобы сделать степень необходимо выделить число, кликнуть по нему правой кнопкой мышки и выбрать «Шрифт».
В результате появится окно «Шрифт». Здесь нужно включить надстрочный шрифт и сохранить настройки нажатием на кнопку «Ok».

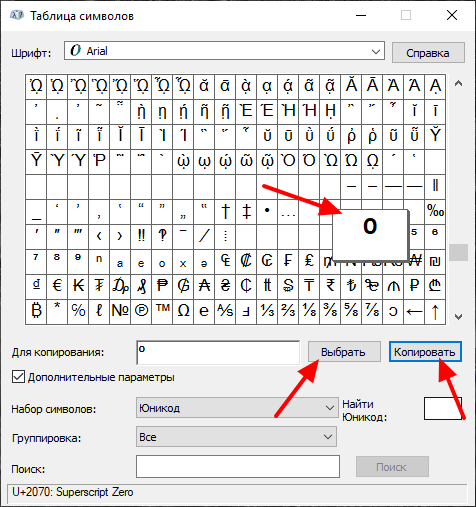
Таблица символов для ввода степени
Ниже приведена таблица символов и сочетаний клавиш, которые можно использовать для ввода степени на клавиатуре:
| Символ | Комбинация клавиш | Описание |
|---|---|---|
| ² | Alt+0178 | Степень в квадрате |
| ³ | Alt+0179 | Степень в кубе |
Таким образом, теперь вы знаете различные способы написания степени числа символами на клавиатуре. Вы можете использовать коды, комбинации клавиш или специальные функции в текстовых редакторах, чтобы правильно обозначить степень числа.

Что нам скажет Википедия?
Маги́ческий, или волше́бный квадра́т — квадратная таблица
n × n, заполненная n^2 различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный натуральными числами от 1 до n^2. Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n^2+1.Нормальные магические квадраты существуют для всех порядков n ≥ 1, за исключением n=2, хотя случай n=1 тривиален — квадрат состоит из одного числа. Минимальный нетривиальный случай показан ниже, он имеет порядок 3.
Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой.
Пандиагональный или дьявольский квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности n=4k+2 (k=1,2,3,…).