Узнайте, какие свойства имеет средняя линия треугольника и трапеции. Узнайте, как с помощью средней линии треугольник и трапеция делятся на равные части и как это помогает в анализе их геометрических свойств.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон. В геометрии средняя линия трапеции имеет ряд свойств и применяется для решения задач и доказательства теорем.

Свойства средней линии треугольника
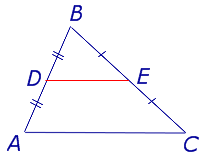
Средняя линия треугольника - это отрезок, соединяющий середины двух сторон треугольника. Согласно теореме, средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Теорема: Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство: Рассмотрим треугольники ABC и DBE. Они подобны, так как имеют две пары пропорциональных сторон (AB = 2BD, BC = 2BE) и общий угол B. Значит, все углы в этих треугольниках равны. ∠BDE = ∠BAC, следовательно, DE||AC по признаку параллельности: соответствующие углы равны. Коэффициент подобия равен 2, значит, AC = 2DE.
Следствие: Три средних линии делят треугольник на 4 равных треугольника ADF, DBE, ECF, DEF. Каждый из четырех треугольников ADF, DBE, ECF, DEF подобен треугольнику ABC с коэффициентом подобия 0,5.
Свойства средней линии трапеции
Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны - боковыми сторонами трапеции. Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
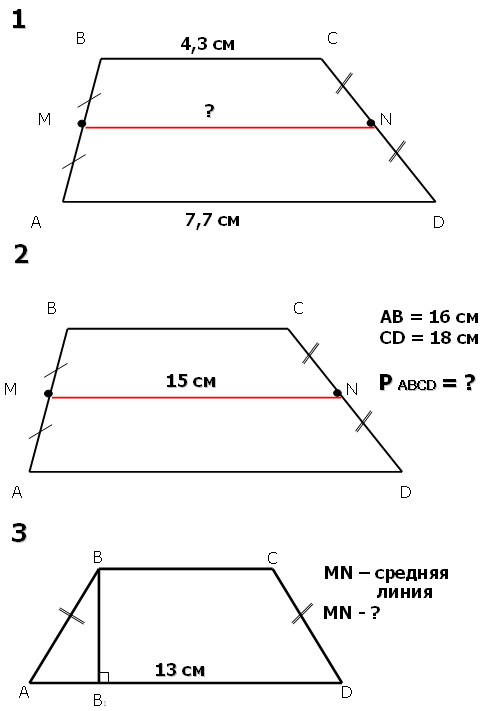
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции.
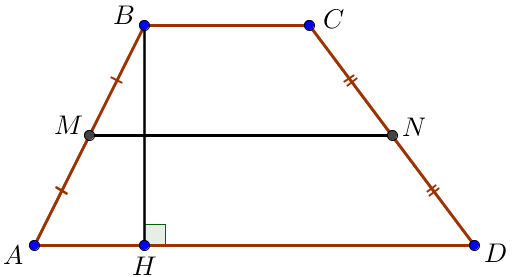
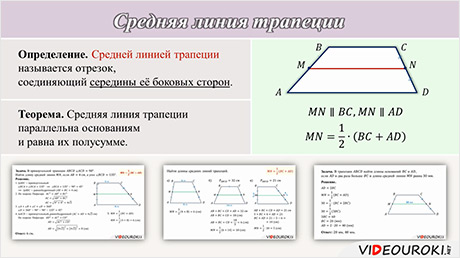
Теорема: Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
Доказательство: Рассмотрим треугольники BCF и FDG. В них CF = FD (по условию), ∠BFC = ∠DFG (вертикальные углы), ∠BCF = ∠GDF (накрест лежащие при параллельных прямых). Следовательно, треугольники равны по второму признаку. Из равенства треугольников следует BF = FG и DG = BC. Значит, отрезок EF является средней линией треугольника ABG. Отсюда следует параллельность: EF||AD||BC. Найдем длину EF. По теореме о средней линии треугольника EF = AG:2 = (AD+DG):2 = (AD+BC):2, что и требовалось доказать.
См. также
Заключение
Средняя линия треугольника и трапеции имеют важные свойства, которые широко используются в геометрии. Знание этих свойств позволяет решать задачи и доказывать теоремы. Благодаря средней линии треугольник и трапеция делятся на равные части, что облегчает анализ их геометрических свойств.

Что нам скажет Википедия?
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон. Согласно приведенным в разделе "Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой" свойствам, средняя линия также проходит через точку пересечения диагоналей и точку пересечения продолжений боковых сторон трапеции.